高卒認定(旧大検)数学 第2回「分数の和差」
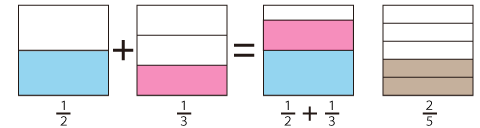
図1を見ると、どう見ても[math]\frac{ 1 }{ 2 }+\frac{ 1 }{ 3 }[/math]は[math]\frac{ 2 }{ 5 }[/math]よりかなり大きいことが分かります。
では、どうすればよいかというと、より細かく分割すればよいのです。2つにも3つにも分割する事が出来る分割の数は、単純にかけ合わせて[math]2\times3=6[/math]分割となります。
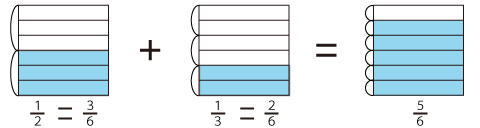
すると、
[math]\frac{ 1 }{ 2 }=\frac{\left(1\times3\right )}{\left(2\times3\right )}=\frac{ 3 }{ 6 }[/math]
[math]\frac{ 1 }{ 3 }=\frac{\left(1\times2\right )}{\left(3\times2\right )}=\frac{ 2 }{ 6 }[/math]
となって、
分母の6は不動で分子のみ足し算して[math]\frac{ 5 }{ 6 }[/math]となります。
つまり分数の足し算をするときには、「分母を同じ数にそろえる。」ということをしなければなりません。このことを「通分する。」といいます。「通分」をもう少し詳しく言うと、「分母を各分数の分母の最小公倍数にそろえる。」ということになりますが、分数が2,3倍など少ない場合は分母をかけることで代用しておきましょう。
前回のクイズの答え
[math]\frac{ 1 }{ 2 }=\frac{ \Box }{ 7 }[/math]
[math]\Box[/math]に入る数は?
ここでは7は2の何倍かということですので、[math]7\div2=3.5[/math](倍)
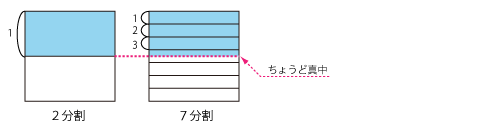
分母、分子に同じ数をかけると[math]\frac{ 1 }{ 2 }=\frac{ 1\times3.5 }{ 2\times3.5 }=\frac{ 3.5 }{ 7 }[/math]となって、[math]\Box[/math]は3.5。
このようにかける数は分数や小数でもOKです。(図3参照)
今回のクイズ
[math]\frac{ 1 }{ 2 }+\frac{ 1 }{ 3 }+\frac{ 1 }{ 4 }=\Box[/math]
[math]\Box[/math]に入る数は?




