高卒認定(旧大検)数学 第9回「正の数・負の数の意味」

数にはすべての人が最初に知ったであろう「[math]1,2,3,4[/math]…」という自然数から始まって、数Ⅰで扱う中で最も広い範囲での「実数」まですべての数は直線状に表すことができます。

その時元になる点は[math]0[/math]とするのが自然ですが、例えば図1のように端を[math]0[/math]としてもいいのですが、直線のどこに[math]0[/math]の点をとっても自由です。（図2）

図1

図2

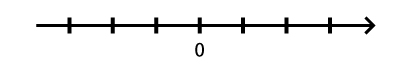
ちなみに、数を表したこのような直線を「数直線」と呼び、右へ行くほど数は大きくなると決めておき、矢印で示します。

また[math]0[/math]（ゼロ）は数の元となるものなので、数直線上で[math]0[/math]を表す点は原点（O：オー）と呼びます。

さて、図2を見ると、Oの左側にも直線が続いています。

この直線状に表される数は先に述べた数直線の決まりからわかるように、「[math]0[/math]より小さい数」となります。これらの数直線上で0の左側にある、[math]0[/math]より小さい数が「負の数」です。

日常の身近なところで例を挙げると、温度がすぐに思い浮かびます。

「明日の朝の最低気温は-5℃でしょう。」

などと天気予報などでも使われていますが、これは摂氏（せっし）という温度の測り方で、水の氷点（ひょうてん：水が氷になる温度）を0、沸点（ふってん：水が沸騰する温度）を100として、その間を100等分、その中の1つを1単位としたものです。

温度にはほかに0点を移動して、氷点を32度、沸点を212度とした華氏（かし）や、数直線の左端を0とした絶対温度K（ケルビン）があります。

まとめ
「負の数とは[math]0[/math]より小さい数」のことです。