高卒認定(旧大検)数学 第5回「分数の積商」

まず整数どうしのかけ算はできるものとします。
例えば、[math]2\times3=6[/math]ですが、整数というのは分母が1の分数ともみなせるのだったから、書き直すと[math]2\times3=\frac{2}{1}\times\frac{3}{1}=\frac{6}{1}[/math]となって[math]\frac{2}{1}\times\frac{3}{1}=\frac{\left(2\times3\right)}{\left(1\times1\right)}[/math]と考えると「分数のかけ算は、分子は分子、分母は分母でそれぞれかけ算すればよい。」ということがわかる。

だから例えば、
[math]\frac{3}{4}\times\frac{2}{5}=\frac{\left(3\times2\right)}{\left(4\times5\right)}=\frac{6}{20}=\frac{3}{10}[/math]となります。
しかし、普通は途中の計算の中で約分して、

[math]\frac{3}{4}\times\frac{2}{5}=\frac{3\times2}{4\times5}=\frac{3}{10}[/math]

となるものです。

割り算の方が少々難しい。
例えば、[math]3\div\frac{1}{2}[/math]を考えると、[math]3[/math]の中に[math]\frac{1}{2}[/math]がいくつあるか、というように考え方を変えると、図のように

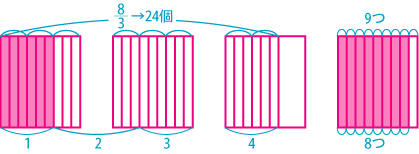
と[math]\frac{1}{2}[/math]は[math]1[/math]の中に[math]2[/math]つあるから、[math]3\times2=6[/math]となるので[math]3\div\frac{1}{2}=3\times2=3\frac{2}{1}[/math]と考えて、「わり算は逆数をかける。」ことになる。逆数とは「分数の分母と分子を入れ換えた数。」です。

例として
[math]\frac{1}{2}\iff\frac{2}{1}=2[/math]
[math]\frac{3}{5}\iff\frac{5}{3}[/math]
など。
同じように[math]\frac{1}{3}[/math]や[math]\frac{1}{4}[/math]など分子が[math]1[/math]のものはできる。

分子が2以上の場合は、その分は普通に整数のわり算と同じように（例えば[math]2\div3=\frac{2}{3}[/math]と÷の後は分母になる。）すればよい。

[math]\frac{2}{3}\div\frac{3}{4}=\frac{2}{3}\times4\div3=\frac{8}{3}\div3=\frac{8}{9}[/math]

[math]\frac{1}{3}[/math]を3つに分けて[math]\frac{8}{3}[/math]全体は[math]\frac{24}{9}[/math]、この[math]\frac{1}{3}[/math]だから[math]\frac{8}{9}[/math]