高卒認定(旧大検)数学 第4回「最小公倍数の求め方」

一番単純な方法は前回使った方法で、クイズの答えでも使っていますが、各数の倍数を書き並べて見比べることで求められます。しかし、この方法は手間と時間がかかります。

そこで計算での求め方を使って2つの数の最小公倍数を求めます。

その1
2つの数をかけて、その2数をわり切れる数(公約数)の中で最大のもの
(最大公約数)でわります。

例)
2数を4と6とすると、4×6=24

4の倍数…4，2，1
6の倍数…6，3，2，1
最大公約数は2だから、24÷2=12で最小公倍数は12

その2
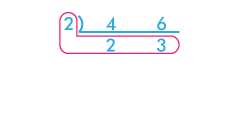
2つの数を並べて、割り算を筆算でするときの記号を逆さにしたような記号を書きます。その2つの両方をわり切る数を左に書いて、割った数を下に書きます。割れる数がなくなったら外側の数を全てかけます。
2×2×3=12となって、これが最小公倍数です。

例)

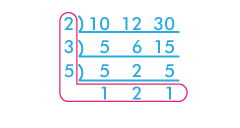
3つ以上の数があるときは、“その1”が使えません。なので、“その2”の改良型というか、少し変わって3つ共通の数は当然ですが2つでも割ってよいことにして、割り切れない数はそのまま下におろすことにします。

下の例は、10，12，30の場合です。上の規則で計算すると、2×3×5×2=60となり、これが10，12，30の最小公倍数です。

例)